Combos Of 4 Binary Options

Over at the SAS/IML Word Forum, someone posted an interesting question about how to create a special matrix that contains all combinations of zeros and ones for a given size.

Specifically, the problem is equally follows. Given an integer
northward
≥ i, produce a matrix with 2
ⁿ

rows and
north

columns that contains all combinations of zeros and ones of length
n. For example, the post-obit matrix is a solution for
n = three:

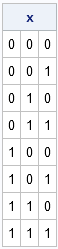
I can think of three ways to reach this job. The start algorithm builds the matrix by columns; the other algorithms build the matrix by rows and, although they are less efficient, they take the advantage of being suitable for a DATA pace implementation.

EDIT:
As of SAS/IML 12.3, you can utilize the EXPANDGRID function to create a binary matrix that contains all binary combinations, For example,
x = ExpandGrid(0:1, 0:1, 0:1);.

Edifice the Matrix by Columns

If you lot written report the example matrix, you will find a pattern to the columns:

1. For the kickoff cavalcade, the first half of the entries contains zeros and the second half contains ones.
2. For the second cavalcade, one-fourth of the entries are zeros, then one-fourth ones, and and then the pattern repeats.
3. For the third cavalcade, one-eighth of the entries are zeros, and so one-eighth ones, then the pattern repeats until all rows are filled.

This suggests an algorithm: for each cavalcade, build upwards a vector that consists of a number of zeros followed past the same number of ones, and and then repeat this pattern until all rows are filled. The length of the pattern depends on the column number. The following module implements this algorithm:

proc iml;   offset GetAllZeroOneComb(n);    rows = 2##n;    /** construct ane column at a fourth dimension **/    x = j(rows, north);    do j = ane to northward;       PatLength = ii##(n-j); /** length of each blueprint **/       PatRepl = ii##(j-ane);   /** number of patterns **/       pattern = j(PatLength,1,0) // j(PatLength,ane,ane);       x[,j] = echo(pattern, PatRepl);    end;    render( x ); finish;   x = GetAllZeroOneComb(3);

You can use the
GetAllZeroOneComb
module to generate matrices of any size. Still, considering the number of rows grows as two
^north
, the algorithm will run out of memory for moderate-sized values of
due north.

Building the Matrix by Rows

If you study the example matrix, y’all will too detect a pattern to the rows: the
ithursday row is the binary representation of the integer
i – i. Therefore an algorithm is to generate the binary representations of the sequence
0:ii##n-1.

I could write a SAS/IML module that takes a number and returns a row vector that contains the binary representation of the number, but instead I’m going to leverage the power of SAS formats. SAS has a BINARYw. format which converts a number into a cord that contains the binary representation of the number. (You lot can utilise the PUTN part to apply a SAS format to elements of a SAS/IML matrix.)

You tin so utilize the SUBSTR function to pick off each character in the binary sequence and the seldom-used NUM function to convert the graphic symbol into a numeric nil or ane. The following module implements this algorithm:

showtime GetAllZeroOneCombByRow(n);    rows = 2##n;    /** construct one row at a time **/    x = j(rows, n);    format = "binary" + strip(char(n)) + ".";    do i = i to rows;       s = putn(i-one, format);       practice j = i to n;          10[i,j] = num(substr(s,j,1));       end;    end;    return( x ); finish;

I don’t like this algorithm for SAS/IML programming because there are no vectors in sight. This is an algorithm that plods through the matrix cell-by-cell and fills in the appropriate zip or one. It is better suited for the Data step than for SAS/IML. In fact, the Data stride implementation is almost identical, except would use an array of variables instead of columns of a matrix.

Edifice the Matrix past Using All Combinations

If the guild of rows in the matrix is not important, then you can implement another row-wise algorithm. I won’t implement information technology here, but yous can use the ALLCOMB function to look at all combinations of
n
elements taken
k
at a time, and apply those combinations equally locations for the ones in the matrix. For example, one of the “iii choose 1” combinations is (two), and this combination corresponds to the row {0 one 0} which has a one in the second location. One of the “three choose 2” combinations is (i, 3), and this combination corresponds to the row {1 0 ane}.

Perhaps you can think of another algorithm? If so, depict information technology in the comments or on the original thread.